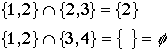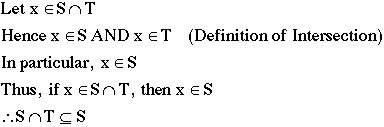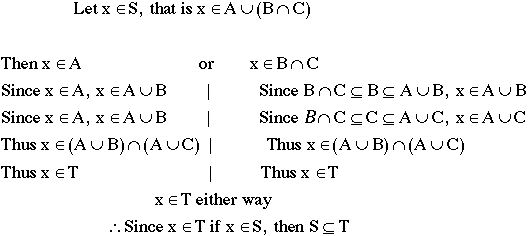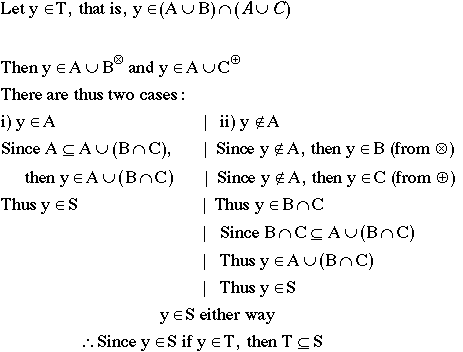Probability and statistics
Set Basics
Definitions
A SET is a collection of Different elements.
Example: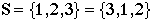 
Note that order does not matter.
We say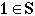 
means "One is an element of S".
and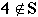 
means "Four is not an element of S".
The EMPTY SET is defined as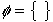 
.
The set of all counting numbers is defined as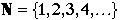 
The complement of a set A, (denoted AC) is defined
as the set of numbers in N not in the original set.
For instance, if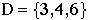 
, then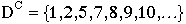 
We also say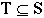 
means "T is a subset of S" if
every element in T is an element in S.
Continuing our example, then, if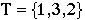 
, then both 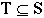and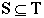 
.
Example: Name all of the subsets of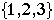 
.
Answer: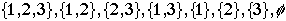 
.
Note that there are eight subsets, one of which is the empty
set. The empty set is a subset of every set, including itself!
We say 
is the number of distinct elements in S. Here,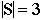
.
Set Operations:
For sets A, B, we define:
UNION:
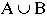= The set of elements in A or B
Example: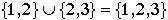 
INTERSECTION:
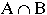= The set of elements in A and B
Example:
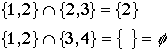
Simple proof involving sets:
Prove: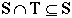 
Proof: We know that for some set to be a subset of another,
every element in the subset must be in the larger (or same-sized)
set. Hence, we look at an element we know is in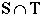 
, and
show that it must be in S. The element we choose will be called x
and will be perfectly general. The following are the steps of the
proof:
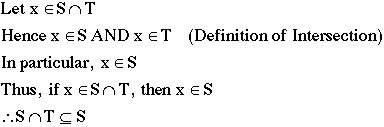
Similarly, we can show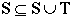 
:
Now for a more involved proof:
Prove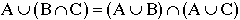 
:
If we call the left-hand side T and the right-hand side S,
then we must show two things to prove equality: first, we must
show 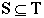; second, we must show .
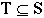1) Prove :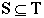
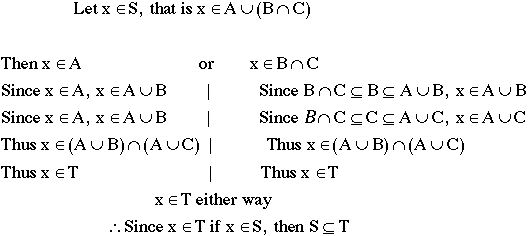
2) Prove :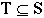
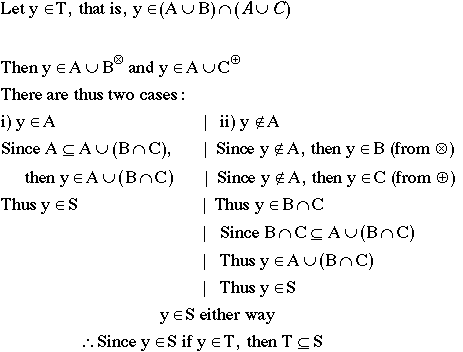
Since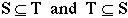 
, then we have proved that S=T, and therefore that , as
desired.
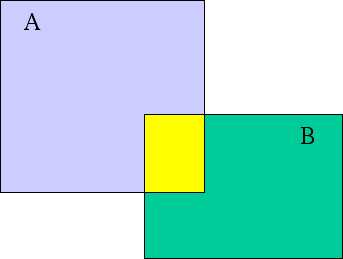
Another way to prove the same thing is to do it graphically,
using Venn Diagrams. In Venn Diagrams, any space inside a closed
shape is assumed to represent elements in that set. The following
diagram shows two sets, A and B; the elements in A are in Blue,
the elements in B are in Green and the intersection of A and B is
colored Yellow.
Now, to prove 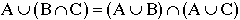, we shade those regions indicated!
:
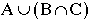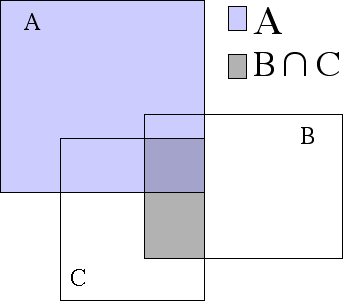
Note than any region shaded is part of .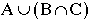
Now, for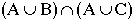 
:
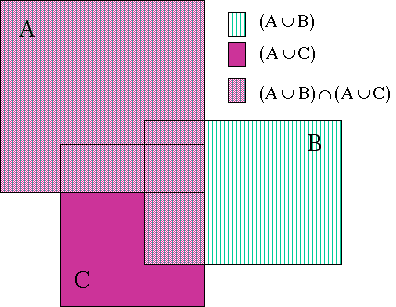
As you can see, the total shaded region from the first graph
is the same as the double-shaded region from the second graph, so
we've proved that .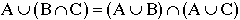
The last topic in basic set theory is the countability
of infinite sets.
Sets come in two flavors: Finite and Infinite.
Finite sets, such as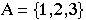 
, has a finite size: 
.
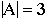An infinite set, such as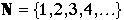 
, has size infinity: 
.
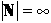Definition: Any infinite subset of N is countable (this
includes, of course, N, since N is a subset of N). What we mean
by countable, then, is a set that can be counted. Physically, if
we had an infinite amount of time, we could count the elements of
N. You can try it some time when you get reeeeealy board: 1, 2,
3, 4. Okay, that's enough for me, but you do see that we could
count all of the elements in N if we had enough time to do so.
Now, since we could count all of N, then obviously, any infinite
subset of N can also be counted. Another way to think of this is
to say that if we can have a one-to-one relationship between N
and any subset, then it is countable. That is, if we look at the
even numbers, then we could count them:
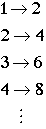
One consequence of this is that any countable subset must be
the same size as N; hence, we see that there are just as many
even Integers as Integers themselves.
So now let's change our definition of countable. Let's say
that any set which can be related one-to-one with N is countable.
So, what other sets are countable?
Let's examine the set of 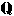Rationals (
). Rational numbers can
be put in terms of p/q (see the page on proofs). Between 0 and 1,
there are an infinite number of Rationals; one example of a
series completely contained between 0 and 1 is 1/2, 1/3, 1/4,
1/5, 1/6, and so on. My claim, however, is that even though there
are an infinite number of Rationals just between 0 and 1, let
alone in and around the rest of the Integers, that there are just
as many Integers as Rationals.
The key here is that I will set up a method for counting the
Rationals, such that I am sure I have counted all of them.
p/q - 1 --- 2 --- 3 --- 4 --- 5 --- 6 ...
1 ---1/1--1/2--1/3--1/4--1/5--1/6 ...
2 ---2/1--2/2--2/3--2/4--2/5--2/6 ...
3 ---3/1--3/2--3/3--3/4--3/5--3/6 ...
. . . . . . .
. . . . . . .
Now, I hope it is plain that all rational numbers can be
listed in this way. So, how do we count them? Start in row 1:
count 1/1. Now start as in the second row and count up and to the
right: 2/1 and 1/2. Next move on to the third row: 3/1, 2/2, and
1/3. Then go on to the fourth row, and so on. We can count every
rational in this way. Since we have shown that we have a
one-to-one relationship between N and the Rationals, then the set
of Integers must be the same size as the set of Rationals (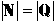
)!
So what about the set of Real Numbers (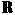
)? Reals include both
the Rationals and Irrationals (non-terminating, non-repeating
decimals). There are an infinite number of them between 0 and 1
as well. To see if they are countable, we can try to count them.
Let's pretend that we can. If this was so, we could out the real
numbers between 0 and 1:
1 -- 0.314159626....
2 -- 0.27182818...
3 -- 0.618033989...
4 -- 0.010011000111...
. .
. .
Now, let's make a number that isn't on the list. If we can do
that, then we must not have listed all of the numbers out. Since
we assumed we had listed them all out, then it must not be
possible to list them. Now, how do we create a number that we are
sure is not on the list? Well, the first digit of the first
number is 3. Let's choose a different number from this for the
first digit of our new number: 4. The second digit of the second
number is 7. Let's choose the second digit of our new number to
be different: 5. The third digit of the third number is 8. Our
new number's third digit should be different: 9. We keep this up
through our whole list. What we come up with is 0.4593... How do
we know that this number is not already on the list? Well, we
know for a fact that every digit of our new number has at least
one digit different from every other number on the list (it is
different from the Nth number in the Nth decimal place!). Since
we just created a number that wasn't on the list, there must be
too many Reals to count. Therefore, there are more Reals than
Integers (even though there are the same number of Rationals as
Integers).
Incidentally, this next level of infinity is denoted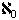 
(aleph naught). 
.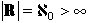