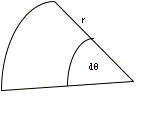
Just like for rectangular coordinates, where weCalculus
Lesson
62
Area
in Polar Coordinates
Back to Dr. Nandor's Calculus Notes Page
Back to Dr. Nandor's Calculus Page
Just like for rectangular coordinates, where we
looked at "differential rectangles" with differential
width, for polar coordinates, we look at
"differential circle sections" with differential angle.
Recall from a circle that the area of a wedge
of the circle is 
.
If we consider
the radius to be constant for a differential
change in angle (just like we did for constant
height given a differential change in x), then
Example: Find the area bounded by the limaçon defined by:
First plot by using various 
values.
When integrating, either use
a table or perform by parts.
Example: Find the area of the inner loop of 
.
First plot, then note that the intersection is at the origin, so we
will integrate with 
When finding intersections, be VERY CAREFUL! In the last example,
we see that when 
,
, so 
we have found two
points
on the curve, 
. If we just
look at the graph, however, it looks like
there are two other points on the graph, but they don't satisfy the equations!
, but we know that 
when 
!
So, we must understand that a polar graph consists of points having
AT LEAST ONE polar coordinate representation satisfying the given equation.
This also means that when we look at two graphs, we may not be able to
solve for their points of intersection just by setting equations equal to each
other, and MUST plot them to check.
Example: 
, DO NOT
have the common point 
.
Only by plotting do we find that they intersect at the origin.
Example: Find the area outside the circle 
but inside the
limaçon 
.
First plot. Set 
s equal to each other to find
intersections, and
check against the graph (no problems with this graph).