.Calculus
Lesson
54
Taylor
Polynomials
Back to Dr. Nandor's Calculus Notes Page
Back to Dr. Nandor's Calculus Page
Before we examine Taylor Polynomials, let's show that
.
Note that this formula only works at x=0!!!!
Let's call 
and 
Note that 
and
and
So, it makes sense that the formula could be right. In fact, this is a good
definition of equivalent functions at a single point. If, at a given point, the
two functions have the same value, and all orders of derivatives evaluated at
that point also have the same value, then the two functions must be
equivalent near that point.
So, we could actually derive this formula! To approximate 
,
Since 
and so on,
then we must make sure the same
is true for 
and so on.
Thus, we can see
This approximation will work well for numbers NEAR 
.
Now, what if we are not looking near 
?
We just do the same thing! 
and so on.
Where 
If we then solve the equations to find all of the ans.
Putting it all together, we come up with the definition of a Taylor Series:
Note, then, that a good choice for 
will be a number for
which we know 
and is near
the x-values we want to look at.
Examples: Find 
through 
for 
about 
.
Find 
for 
about 
(Maclauren polynomial).
Find 
for 
about 
.
Find an approximation for 
using
the Maclauren polynomial
to 5th order (use 
about
).
Now how accurate is this approximation? Let's say that 
where 
is evaluated
at 
. The error is 
, where
. Note that this is
just the next term of the
Taylor Polynomial, evaluated at 
.
If we plug all possible 
s
into the
remainder, we have a range of error for our approximation. It turns out that
there will always be a possible 
such that 
(or 
)
Taylor's Theorem says that there exists some 
for which the above is
true.
Therefore, if we plug in the bounds for 
, we get the range of errors.
Example: Find 
using
the Maclauren polynomial to 5th order , and
determine the possible range of error on the approximation.
about 
where 
since 
and 
(Maclauren polynomial!)
The largest error would occur if 
,
so
Therefore, we can conclusively say that:
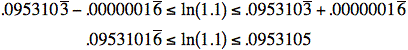
So to 6 decimal places, 
According to our calculators, 
Example: Using 3rd order Maclauren series, find 
and estimate error
(remembering 
).
So 
The remainder is 
where
.
The largest remainder occurs when 
Now, we don't know
what 
is, since
that's what we're trying to find! However, we can definitely say that
, so let's stick that in.
Therefore,
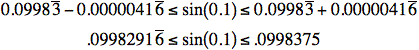
So to 5 decimal places, 
According to our calculators: 