Calculus Methods
32 Generating Taylor Series and Taylor Polynomials
Unless you have a function that is almost already in the form
of a geometric series (see method 31), then you'll use the
Taylor Series method, although you may use the Taylor Series
method for any series you would like: it works in all cases.
1) Find the first n derivatives, as required by the problem. If you
are finding the series representation, calculate as many derivatives
as you need to find the pattern.
2) Evaluate each
derivative at the value, 
,
about which the power
series will be centered.
3) The power series is
found by the formul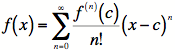a: 
. A
Taylor Polynomial of degree n is denoted 
and comprises only
terms up through the 
.
4) The series
converges when remainder goes to zero, 
for any x in the interval. However, just as with any power series,
we can simply find the Interval of Convergence (see method 30)
the same we did before. For approximating answers with Taylor
Polynomials, the definition of the remainder is
, where 
or 
.
When approximating
error, remember to use the value of z that yields the worst possible
error to be on the safe side!
Example #1: Find the Taylor Polynomial of degree 4 for the
function 
, centered about 
.
Use 
to approximate 
.
1) First, our list of derivatives (in this case, they are very simple):
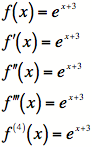
2) The derivatives
evaluated at 
(our center
for this problem is
).
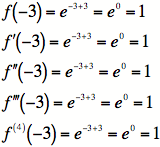
3)
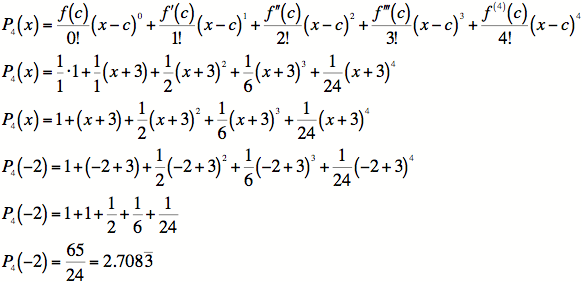
4) We must find the
remainder, 
, but that
means we must take one more derivative.
Now we must pick the
value of 
that gives
us the largest
possible value of 
.
Simply plugging in the endpoints, we
find 
.
We know the
exponential function is always increasing, so the maximum value
occurs when 
. And here is where
things get sticky. Assuming
we don't have a calculator (the whole reason we need to
approximate!), we do not know what the value of e is! However,
we do remember that it is less than three. So we'll use the fact that
to give ourselves a decent
approximation.
At worst, then, our remainder is
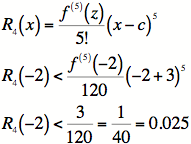
So our approximation is:
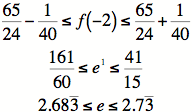
We could do better assuming e is in between those values and
re-figuring 
, but this approximation is good enough.
The
actual value, incidentally, is 
,
which is clearly between
the two values listed above.
Example #2: Find the
Taylor Series for 
about the
point
.
1)
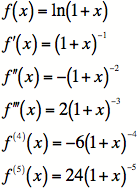
The pattern here is fairly easy to see at this point, so we'll move on.
2)
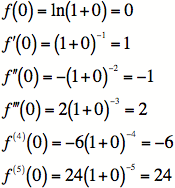
At this point, it's
fairly clear that the 
term will be
or 
We would typically use the former, since the form of the exponent
then matches the form of the factorial, but there is no really hard
rule.
Also note that since
the 
term is 0, that we
will not include that
term in our summation.
3) Here is the Taylor Series:
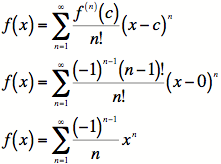
4) Using the Ratio
Test, we find that our Radius of Convergence is 
:
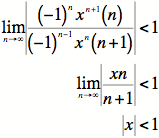
Since we are centered
about 
, our endpoints are 1
and -1. To
test them, we plug them in:
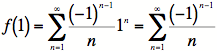(Alternating Harmonic Series: converges)
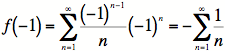(Harmonic Series: diverges)
Finally, then, our
answer is:
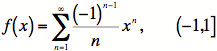
Back to Dr. Nandor's Calculus Methods Page
Back to Dr. Nandor's Calculus Page