Calculus
Methods
22 Volume
There are two typical volume problems: volumes of
revolution and volumes by cross-section. There are too many
exceptions to cover in a single web-page, so amazingly broad
generalizations will be used here. The only way to really get a
handle on the way to find volumes is to do lots of practice
problems.
1) Volumes of revolutions: regions revolved about a horizontal
line.
1A) Sketch a graph; it does not have to be very accurate, but
the endpoints should be calculated and the general shape
should be drawn.
1B) We will be using discs or washers. Draw a thin rectangle
that represents an edge-on view of the cross-section. Next to
this, beside the drawing, draw either a circle (disc) or an
annulus (washer). Include variables 
for a disc or 
and 
for a washer.
1C)
Write down the differential volume equation 
for a disc or 
.
1D) Comparing the picture of your cross-section to the
picture of your rectangle,
substitute in for 
for discs or 
and 
for washers. Make sure that if you now have 
s
in your
differential volume, that you replace them with the
respective
functions in terms of 
so that integration
is
possible. Always draw arrows and compute quantities as they
refer to the original function (see examples)!
1E)
Determine the values of possible 
s,
which will become
the limits of the integral.
1F)
Integrate 
or 
.
2) Volumes of revolutions: regions revolved about a vertical line.
2A) Sketch a graph; it does not have to be very accurate, but
the endpoints should be calculated and the general shape
should be drawn.
2B) We will be using cylindrical shells. Draw a cylinder in
the drawing. Include
the variables 
(the radius of the
cylinder) and
(the height of the
cylinder).
2C)
Write down the differential volume equation
.
Some students in the past have pointed out that they
remember the equation as
"two pi PhD p." Yes, the 
is
a rho
(for radius) and not a 
, but it's a
decent mnemonic for them.
2D) Considering the picture of your cylinder, middlestitute in for
, ,
and 
. Make sure that if you now have 
s in your
differential volume, that you replace them with the
respective functions in terms of 
so that integration is
possible. Also note that 
represents the thickness of the
cylindrical shell; since this thickness is a differential
difference in the x-direction, 
is
identical to 
. Always
draw arrows and compute quantities as they refer to the
original function (see examples)!
2E) Determine the values of possible radii, and observe to
which 
s these correspond; these 
s will become the limits of
the integral.
2F)
Integrate 
3) Volumes by cross-section.
3A) Sketch a graph; it does not have to be very accurate, but
the endpoints should be calculated and the general shape
should be drawn.
3B) We will be using SOME sort of cross-section. The
problem will tell you what the cross-section is; common
cross-sections are discs, squares, semi-circles (which really
should be called hemi-discs or semi-discs, but the AP Exam
will rarely call them this), isosceles right-triangles with either
a leg on the base or the hypotenuse on the base, and
equilateral triangles. Draw a thin rectangle that represents an
edge-on view of the cross-section. Next to this, beside the
drawing, draw a picture of the cross-section. Be sure to
include all appropriate variables. Also be careful to make the
rectangle in the correct direction. If the cross-sections are
perpendicular to the x-axis, they should be vertical.
3C)
Write down the differential volume equation 
or
, depending on whether the
cross-sections are
perpendicular to the x-axis (dx) or whether they are
perpendicular to the y-axis (dy). In each case, A is the area
of the particular cross section at which you are looking.
3D) Comparing the picture of your cross-section to the
picture of your rectangle, substitute in for whatever variables
exist in your cross-section. Make sure that if you now have
s in your differential
volume, that you replace them with the
respective functions in terms of 
so that integration is
possible.
3E)
Determine the values of possible 
s
or 
s, which will
become the limits of the integral.
3F)
Integrate 
or 
.
Example
#1: A region is bounded by 
, 
, and the x-axis.
Calculate the volume that results when this region is rotated about
the line 
.
1)
The line 
is a horizontal line,
so we will use discs or
washers.
1A)
The general shape of 
is:
When bounded by the other lines, the resulting region is:
When
we rotate this about the line 
, we get a
graph that
looks like this:
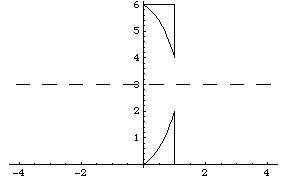
Of course, in reality, it would look like some sort of doughnut
or washer with a flat bottom and a sloped top (as seen from
above).
1B) Since the figure has parts that are not connected, we will
be using washers.
1C)
1D)
The larger radius, 
, is the distance from
the line 
to
the x-axis, and
this distance is always 3. So 
. The
smaller
radius, 
, is the distance from
the line 
to the function
. So 
.
1E)
In this case x runs from 
to 
.
1F)
Example
#2: A region is bounded by 
, 
, and the x-axis.
Calculate the volume that results when this region is rotated about
the line 
.
2)
The line 
is a vertical line,
so we will use cylindrical shells.
2A)
The general shape of 
is:
When bounded by the other lines, the resulting region is:
When
we rotate this about the line 
, we get a
graph that
looks like this:
Of course, in reality, it would look like some sort of doughnut
or washer with a flat bottom and a sloped top (as seen from
above).
2B)
 |
2C)
2D)
Examining our picture above, 
, 
(look
carefully and you'll see it), and
. So our new equation is
. Finally, we must rid ourselves of y.
In
this case, y is simply the upper function, so our final equation
is 
.
2E)
All of the possible radii stretch from 
to
. The 
s
we will use run from 
to 
. We can test that this works
by look
at our radii. When 
, 
; when 
, 
. So
we're all set.
2F) Integrating:
Note that the answers for examples one and two are
different! They are different shapes and have different
volumes!
Example
#3: A region is bounded by 
, 
, and the x-axis.
Calculate the volume that results when this region is the base of a
solid, and each cross section of the solid perpendicular to the x-
axis is an equilateral triangle.
3) We are working with volumes by cross-section.
3A)
The general shape of 
is:
When bounded by the other lines, the resulting region is:
To see the 3-dimensional object accurately, click here.
Otherwise, let's continue.
3B) Make sure that you draw the triangle in the correct
direction! One of the sides of the triangle MUST be the same
as the "little rectangle" height. Also make sure that you draw
the rectangle in the correct direction. It must be
perpendicular to the x-axis!
3C) The differential thickness is in the x-direction, so our
differential volume
is 
.
3D)
Examining the picture above, we see that 
.
From
what we know about equilateral triangles, we also have that
the area is 
. Combining this information, we get
find
. We will be integrating with respect
to x, so we
must change our y into x. Our final differential volume of
.
3E)
The 
s run from 
to 
.
3F) Integrating:
