Calculus Methods
06 Solving Related Rates Problems
1) Draw a picture, if applicable, labeling all
quantities.
2) Write down what rate the question requires you
to find.
3) Write down everything you already know from
the information provided in the problem EXCEPT
for any quantities that only apply at the end of the
problem (for example, if the problem asks you to
find how fast the water level is rising after 39 days,
DO NOT write down that time=39 days. This only
applies at the END of the problem, and does not
affect how the problem is solved until you plug it in
at the end).
4) By this time, you should have written down a
rate that you need to find (in step 2) and a rate that
you already know (in step 3). The "hard" part of the
problem is now this: find an equation that relates
the two variables involved in those two rates (for
example, if you know
and you are looking for
,
you must find an equation relating
and
. If
the
equation has other variables in it, you must use the
other information given in the problem to reduce
the equation down to two variables only: the one
involved in the rate you are looking for and the one
involved in the rate you know.
5) Take the derivative of both sides of the equation
you found in step 4, WITH RESPECT TO "t". Use
implicit differentiation (see method 05) if necessary.
6) Solve the equation for the rate for which you are
looking.
7) Plug in any end-of-problem numbers (see step 3).
8) Write a sentence to explain your answer, so that
a 3rd grader would understand it. For AP tests, this
is a must, so that the AP graders know that you
know what's going on.
Example
#1: A square's area is increasing at
.
What is the rate of change of the square's side
length when the area of the
square is
?
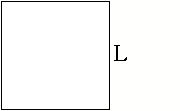1)
2)
The rate we are trying to find is
.
3)
The rate we know already is
. We DO NOT
write down the ending area, as we do not need that
information until the end. For such a simple
problem, this is the extent of what we know.
4)
The two variables involved in the two rates are 
and 
. For a square, there is a simple
relationship
between these two variables: 
.
5)
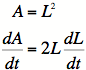
6)
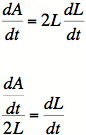
7) Note that the ending value given is for area,
whereas we have side length in our equation. We
can either substitute side-length into our equation
for area, or we can calculate the ending value of the
side length based on what the ending value of the
area is. Either way works.
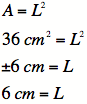
The last step is valid (and needed) since side length
must be positive!
To finish:
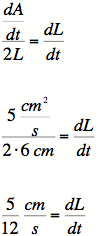
8) Make sure that you include the ending condition
in the sentence and to say whether something is
getting bigger or smaller. Here is an example of a
good sentence:
"When
the area of the square is 
, the
side length of the square is getting bigger at a
rate of 
."
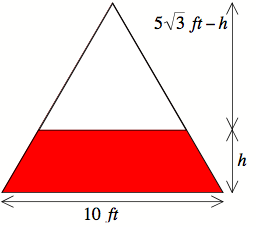
Example #2: A school in Egypt is raising money and
they want to chart the results using an equilateral
triangle, wide at the bottom and pointed at the top.
The area of the triangle filled is proportional to the
amount of money that comes in. The triangle on the
chart has a side length of 
(it's near the lacrosse
field). The top of the triangle represents a total of
$1 million and the bottom represents $0. The money
comes in at a constant rate
of 
. At what rate
is the
"filled" level rising when 
have
been
collected? At what rate is the "filled" level rising
when 
have been collected? At what rate is
the "filled" level rising when 
have
been
collected?
Don't be daunted by the size of the problem! Just
take each step, one-at-a-time!
1) We know the total height of the of the triangle is
2)
We are looking for 
.
3)
We know the rate 
and nothing else.
4) For this problem, we need an equation relating
money and h. We do not immediately have such an
equation in our arsenals, so we need to attack the
problem in some other way. We do have an
equation that can relate height to area, and we can
find an equation that can relate money to area, so
we'll start there.
The
total area of the large triangle is 
,
and the
total amount of money is 
.
Since money is
proportional to area, we know:
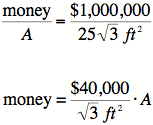
The area of an equilateral triangle of height h is
easily found with our knowledge
of 
triangles, and the red area is simply the total triangle
area minus the white triangle area.
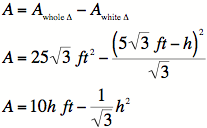
So now we have two equations that we can combine
into a single equation relating money and height.
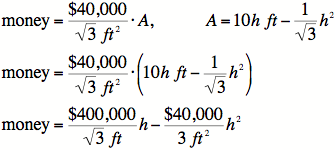
5)
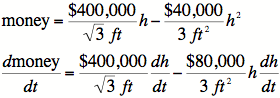
6)
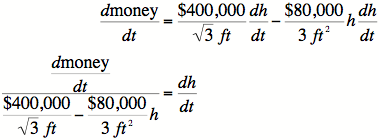
7) Before we can plug in for h, we must determine
what h is! Solving the quadratic equation we found
in part 4, we find that when the money is
, that 
.
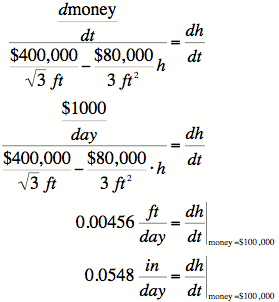
When
(and therefore 
),
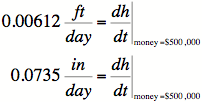
When
(and therefore 
),
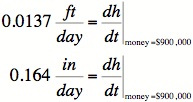
8) A good sentence for the last result would be:
"When $900,000 have been
collected, the height of
the triangle is rising 0.164 inches per day."
On to Method 07 - Finding Absolute Extrema
Back to Dr. Nandor's Calculus Methods Page
Back to Dr. Nandor's Calculus Page